STABILITY
ANALYSIS FOR THE SUBMERGED REEF BALL BREAKWATER PROPOSED FOR THE <UNDISCLOSED
HOTEL>RESORT, qUINTANA rOO, mEXICO
Performed by: Dr. Lee E. Harris, Ph.D., P.E.
Associate Professor of Ocean Engineering & Oceanography
Division of Marine & Environmental Systems
Florida Institute of Technology
Melbourne, FL 32901 USA
Performed for: Ing. Jose Enrique Chacon Gonzalez
Marenter, S.A. de C.V.
Cancun, Q. Roo, Mexico
1. Introduction
This report presents the results of a stability analysis performed for the proposed submerged artificial reef breakwater for the <UNDISCLOSED HOTEL>Resort being constructed near Playa del Carmen in the Mayan Riviera corridor south of Cancun, Mexico. The purpose of the proposed Reef BallTM installation is to reduce the wave energy reaching the shoreline in this area, and to stabilize the sandy beaches landward of the breakwater.
Wave tank stability tests of Reef BallTM units were performed at Florida Institute of Technology in Melbourne, Florida, under the supervision of Dr. Lee Harris. The wavetank tests were used to determine the magnitude of the waves necessary to create movement (instability) of the Reef BallTM units.
2. Wave Force Calculations
The basic equation for the stability of submerged objects is the Morison Equation The total horizontal wave induced force on a submerged object can be broken up into two basic parts as can be seen in Equation 1:
![]()
The Morison equation can then be further expanded to reflect the balance between the lateral wave forces and the resisting forces. The sole resisting force for an object resting on the sea floor is the weight of the object. Now assuming that the object remains stable until the point that the wave forces become greater than the resisting forces, the Morison Equation can be rewritten as Equation 2:
![]()
Equation 2 is the basis for determining the stability of objects resting on the sea floor.
2.1. Drag Force
The drag force is the predominate wave induced force on a submerged object in shallow water (Dean). The drag force is calculated using the classic drag equation (Roberson) as seen in Equation 3:
![]()
Where CD is the coefficient of drag, r is the density of sea water, and Ap is the projected cross sectional area as seen from the direction of flow, and U is the maximum horizontal water particle velocity. The only unknown in the equation is the coefficient of drag. Since the coefficient of drag is dependent on the shape and surface roughness of the object, it must be determined experimentally. Results of the scale model tests are used to determine the drag coefficient.
The maximum horizontal water particle velocity, U, can be determined using the following equation based on linear wave theory (USACE):
|
Equation 4 |
![]()
Where H is the wave height, T is the wave period, d is the water depth, z is the depth at which the water particle velocity is calculated, and k is the wave number. The cosine term is the wave phase which is set to 1 to calculate the maximum particle velocity.
2.2. Inertia Force
The inertia force is the force imparted on the submerged object by the acceleration of the fluid past the object. The inertia force is defined by Equation 5 (Dean)
![]()
Where CM is the coefficient of inertia, r is the density of sea water, Vol is the volume of the submerged object, and a is the water particle acceleration.
The coefficient of inertia is based in the size and shape of the object. CM is always greater than or equal to one. A general equation for CM is given below (Dean), where km is the added mass term whose value is determined by the shape of the object:
|
Equation 6 |
![]()
A widely used value for km is 1 for an object with a circular cross section.
The horizontal water particle acceleration (a) is calculated using the following equation (USACE):
|
Equation 7 |
![]()
where H is the wave height, g is the acceleration due to gravity, L is the wave length, k is the wave number, d is the water depth, and z is the depth at which the acceleration is calculated. The sine term is set to 1 to calculate the maximum particle acceleration.
3. Resisting Forces
The resisting forces are what keep the submerged object from moving due to the wave induced forces. For the case of an object resting on the sea floor without any form of anchoring, the sole resisting force is the weight of the object. There are two forces which lessen the resisting force of the submerged object.
3.1. Buoyancy Force
First is the buoyancy force which is defined in the following equation (Archimedes):
|
Equation 8 |
![]()
3.2. Lift Force
Next is the lift force. As in an airfoil, as the water flows over top of the submerged object resting on the sea floor, a lift force is developed.. The general equation of lift is given in Equation 9 (Roberson):
![]()
Where CL is the coefficient of lift, r is the density of sea water, S is the planform area of the submerged object, and U is the horizontal water particle velocity. To calculate the maximum lift force, the maximum water particle velocity will be used in the stability analysis.
3.3. Sliding Friction
Assuming that the submerged object is resting on the sea floor and that the only form of movement due to the wave induced forces will be in the horizontal direction (sliding), the resistance to movement is further decreased by the coefficient of friction (m). The coefficient of friction is dependent on which two materials sliding are over each other. For several wave tank tests, the models were tested on a smooth, hard plastic bottom and a sand bottom.
In order to determine a value for the coefficient of friction a simple test was conducted. A spring scale was attached to the artificial reef model and pulled horizontally across a submerged surface. The force required to initiate movement of the model was recorded. This force is then divided by the normal force (submerged weight) of the model which results in the coefficient of friction. The tests results were as follows:
m = 0.4 for concrete sliding on hard plastic
m = 0.5 for concrete sliding on submerged sand
From this information, a basic equation for the resisting force can be written as follows:
![]()
4. Factor of Safety
A factor of safety (FS) is used to account for the unknowns and unforeseen circumstances which my occur in the analysis. Although several assumptions have been made thus far, it is necessary to add a general factor of safety to the analysis. There are two unknowns in the stability analysis which will require the use of a safety factor. First is the coefficient of inertia (CM). Since there is little published data on values for CM for complex three dimensional shapes such as artificial reefs, it is necessary to make an estimation. The second and more significant unknown is the coefficient of drag (CD). Wave and wind tunnel tests were conducted to determine values for CD, and values used in the calculations must also include consideration of biological growth such as coral. The coefficient of drag is highly dependent on the surface roughness. The increased roughness due to biological growth on the reef unit, will cause the coefficient of drag to increase, consequently increasing the drag force.
The Factor of Safety is inserted into the Morison Equation (Equation 2) resulting in Equation 11.
![]()
5. Settling
The stability of the artificial reef may be increased due to the settling of the unit into a soft bottom, such as sand. The increased water particle velocity due to the fluid traveling around the unit, can cause sediments to erode from around and underneath the base of the unit, thus allowing the unit to settle into the bottom. Settling reduces the cross sectional area used in calculating the drag force as well as creating the added resisting force of the sediments surrounding the modules. For the purposes of the stability analysis, the worst case scenario must be tested, thus the assumption that there is no settling occurring must be made.
6. The Stability Equation
The stability equation can now be derived from the equations described previously. The first step is to substitute into the Morison Equation, Equation 2. By adding Equation 10 and Equation 11 to Equation 2, the stability equation can be written as Equation 12.
![]()
In order to make this equation more usable, it must be rearranged such that the use of the equation will yield results which are clear, easy to understand, and in terms of one variable. There is only one variable in Equation 12 which is not determined during the analysis, the module’s dry weight. Rearranging yields Equation 13:
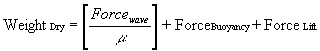
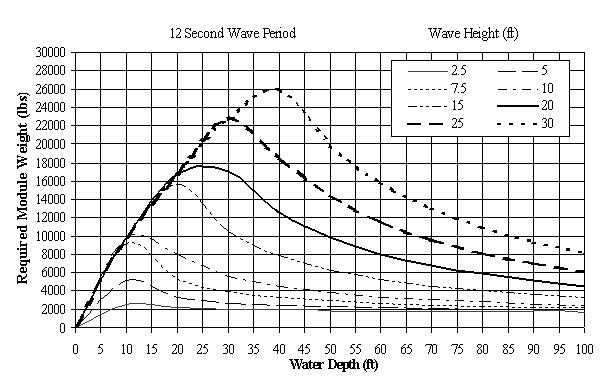
Equation 13 is the final stability equation used in the stability analysis. Results are plotted graphically with the water depth on the X axis and the required module weight on the Y axis. A graph was generated for each design wave period, and each graph has multiple stability lines for different wave heights.
Figure 1 shows the stability graph for a Reef BallTM unit for waves with 12-second periods. The required module weight is the minimum required dry weight of an individual unit so that it will be stable against sliding due to its weight and friction with the bottom, for a hard bottom. For a sand bottom, unit settlement into the bottom would increase the resistance to sliding.
Figure 1: Reef BallTM Stability Curves
7. <UNDISCLOSED HOTEL>Site Design
For the <UNDISCLOSED HOTEL>site, Reef Balls will be placed in water depths of 1.4 to 1.8 meters (5 to 6 feet) at low and high tides, respectively. This design depth range results in a breakwater with a ratio of structure height to water depth = h/d = 0.8 to 0.67, respectively, which is the minimum ratio recommended for wave attenuation. For normal water level and wave conditions, the maximum wave height can be calculated as 0.78 times the water depth resulting in a design wave height of 1.4 meters or about 5 feet. Wave parameters were determined using ACES software (USACE), which resulted in calculated values of wavelength = 50 meters, maximum horizontal water particle velocity = U = 1.65 m/s and maximum horizontal acceleration = a = 1.0 m/s2.
7.1. Stability Analysis
Stability analysis for Reef BallTM unit resistance to movement by waves was performed. Analyses were performed for (1)resistance to sliding due to the submerged weight of the unit and friction with the bottom and (2)resistance to sliding using rebar through Reef BallTM units into the rock bottom. These results are presented in the following sections.
7.1.1. Resistance to Sliding due to Friction and Weight
For waves with 12-second periods, Figure 2 above shows that the minimum required weight of an individual Reef BallTM unit necessary to resist sliding is approximately 4,000 pounds. Applying a safety factor of 1.5, the recommended design weight of an individual Reef BallTM unit to resist sliding under normal maximum wave conditions is 6,000 pounds = 3 tons.
7.1.2. Resistance to Sliding using Rebar through Reef BallTM Units into Rock Bottom
The Morison equation can be used to determine wave forces on an individual Reef BallTM unit. For the 12-second 1.4-meter wave height, the results are 7 kN for the drag force and 10 kN for the inertial force. Since these forces are not in phase, the total combined wave force can be determined as 13 kN for the largest non-breaking wave.
For breaking waves, the Shore Protection Manual (USACE) provides an equation for determining the force per unit length = f as:
![]() Equation 14
Equation 14
Using Hb = 1.4 meters and the width of the Reef BallTM unit =1.8 meters = D yields a breaking wave force of 22.2 kN/m, and for the height of the Reef BallTM unit = 1.2 meters yields an overall horizontal wave force of 26.6 kN, which is twice the non-breaking wave force calculated above. Therefore the rebar will be designed to resist the shear force due to the 26.6 kN breaking wave on the Reef BallTM unit.
The rebar will be subjected to this horizontal shear force from the wave force on the Reef BallTM unit. Using a safety factor of 2 results in a total design shear force of 53.2 kN = 5430 kgf = 12,000 pounds, neglecting any frictional force between the Reef BallTM unit and the bottom.
Using a working shear stress of 10,000 psi for the rebar would require a total cross-sectional area of 1.2 square inches (12,000 pounds divided by10,000 psi). Using four rebar requires each rebar to have a cross-sectional area of 0.3 square inches, which is equivalent to a diameter of 0.62 inches (for which 5/8-inch number 5 rebar can be used).
Note that this analysis includes a factor of safety, and neglects the frictional force between the Reef BallTM and the bottom. In reality, the combination of the weight using 6,000 pound Reef BallTM units plus the rebar to resist sliding provides more than the required stability.
8. Conclusions and Recommendations
Recommended design of the Reef BallTM artificial reef submerged breakwater is five or six rows of units, placed in a water depth of 1.4 meters below low tide (1.8 meters at high tide). The Reef BallTM units should be fabricated with the maximum amount of concrete, so that individual 1.2 to 1.4 meter high units weigh a minimum of 6,000 pounds each. Anchoring to the bottom using four 5/8-inch diameter or greater fiberglas rebar is recommended for additional stability of the units, especially for the units comprising the seawardmost and landwardmost rows.
Wave and water levels greater than those used in these design calculations, such as those associated with major hurricanes, can produce much greater forces which could produce instability and movement of the Reef BallTM units. Ships, boats, and other large water-borne objects may damage the units, and the breakwater area must be adequately marked for the safety of boaters and swimmers.
9. References
Dean, Robert and Dalrymple, Robert. Water Wave Mechanics for Engineers and Scientists. World Scientific, New Jersey, 1991.
Nielsen, P.N. “Explicit Solutions to Practical Wave Problems”. Proceedings 19th Conference on Coastal Engineering, ASCE, V1, 968-982. 1984.
Reef Ball Home Page. http://www.reefball.org
Roberson, John and Crowe, Clayton, Engineering Fluid Mechanics. Houghton Mifflin Company, Boston, MA. 1990.
U.S. Army Corps of Engineers. Automated Coastal Engineering System (ACES). Coastal Engineering Research Center, Waterways Experiment Station, Vicksburg, Mississippi. Version 1.07e 1994.
U.S. Army Corps of Engineers. Shore Protection Manual. Coastal Engineering Research Center, Waterways Experiment Station, Washington, D.C.: U.S. Government Printing Office. 2 Vols 1984.