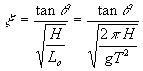BREAKWATER WAVE ATTENUATION

BREAKWATER GEOMETRY

The main parameters used to describe the general geometry of a submerged breakwater are shown in Figure 1. These include the height of the structure = h, water depth at the toe of the structure = d, and the freeboard of the structure = F, where the freeboard is the difference between the height of a breakwater structure and the water depth at the seaward toe of the structure. The slope of the seaward face of the breakwater is tan q, and the offshore slope of the bottom seaward of the structure is tan b = m, which is zero for a horizontal sea bottom.

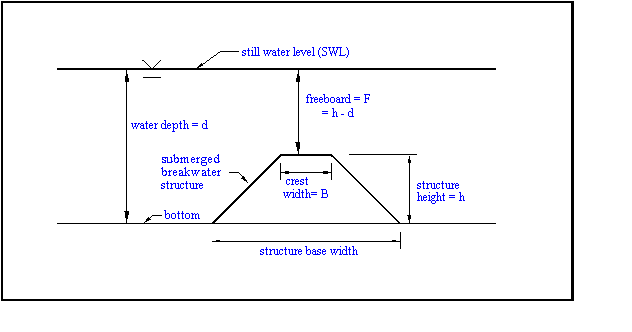
Figure 1. DEFINITION SKETCH FOR A SUBMERGED BREAKWATER

One of the most important parameters for the design and effectiveness of a breakwater is the degree of emergence or submergence. This can be expressed by three different dimensionless terms:

1. the degree of submergence = d/h ;

2. the relative structure height = h/d ; and

3. the relative freeboard to water depth ratio = F/d .

The degree of submergence is the ratio of the water depth to the height of the structure. For an emergent or subaerial structure, whose crest height exceeds the water depth, this ratio is less than one (d/h < 1.0), and for a submerged structure, this ratio is greater than one ( d/h > 1.0).

The relative structure height, which is the ratio of the structure height to the water depth (h/d), also can be used as a dimensionless parameter to express the degree of emergence or submergence of a breakwater. The relative height has a value that is less than one (h/d < 1.0) for a submerged structure, and greater than one (h/d > 1.0) for a subaerial or emergent breakwater.

The freeboard is defined as the structure height minus the water depth,

F = h - d [1.],

where F is the freeboard, h is the height of the structure above the bottom, and d is the water depth at the seaward toe of the structure. An emergent or subaerial breakwater has a positive freeboard value, and a submerged breakwater has a negative value for the freeboard. The dimensionless parameter for the relative freeboard is the freeboard ratio, which is defined as the freeboard divided by the water depth,

[2.].

With this definition of the freeboard ratio, an emergent or subaerial breakwater has a positive value for the freeboard ratio (F/d > 1.0), while a submerged breakwater has a negative value for the freeboard ratio(F/d < 1.0).

These three dimensionless quantities, d/h, h/d, and F/d, indicate the relative height of the breakwater compared to the water depth, and are used to determine the magnitude of the wave and current forces on the breakwater, and the effectiveness of the structure in attenuating wave energy. A classification scheme is formulated later in this study to quantify these relationships.

BREAKWATER RELATIVE CREST HEIGHT

Another important dimensionless parameter used for determining the interaction between the waves and a breakwater structure is the freeboard divided by the wave height, which can be expressed as:

[3.],

where H is the height of the wave, measured from the bottom of the trough to the top of the crest. The use of the wave height in this ratio provides a direct comparison between the height of the structure above or below the still water level, and the height of the waves impacting the structure. Note that this ratio is equal to the ratio of the structure height to incident wave height minus the ratio of the water depth to the incident wave height.

For a submerged structure, the freeboard and freeboard ratios F/d and F/H all have negative values, and the structure is continuously overtopped by waves. The more submerged the structure is, the more negative the ratio of the freeboard to the wave height, and the interaction between the waves and the structure will decrease.

For an emergent structure that has a positive value of freeboard, F/H is also positive. When the ratio F/H is less than one (F/H <1.0), the structure is easily overtopped by the waves, and significant wave transmission past the structure by overtopping occurs (Ahrens, 1987). When F/H is greater than one (F/H >1.0), the structure height is at least one wave height above the still water level, and most of the wave energy is absorbed and attenuated by the structure. Some wave energy still may be transmitted through the structure if the structure is porous, and some wave energy may be transmitted over the structure by wave overtopping (U.S. Army Corps of Engineers, 1984).

WAVE PARAMETERS

Other dimensionless quantities are used to compare the wave height to the water depth, and to determine the type of wave relative to the water depth. The ratio of the water depth to the wavelength (d/L) is used to determine the relative depth of the water compared to the length of the waves. For a ratio of d/L greater than one-half, the waves are considered to be in deep water, and for a ratio of d/L less than 1/25, the waves are considered to be in shallow water (U.S. Army Corps of Engineers, 1984).

The dimensionless parameter H/d is used for the relative height of the wave compared to the water depth, and is often used to determine wave breaking criteria. For a smooth, flat slope, the maximum ratio of H/d = 0.78 is commonly used for wave breaking criteria, and increases as the bottom slope increases (U.S. Army Corps of Engineers, 1984).

The surf similarity parameter, also known as the surf parameter or Irribarren Number, is a dimensionless parameter that is used to describe the characteristics of ocean wave phenomena. The surf similarity parameter is defined as

[4.],

where H is the incident wave height, T is the wave period, g is the acceleration of gravity, tan q is the slope of the sea bottom or structure slope, and L_o is the deep-water wavelength, where L_o = gT² /2p using linear wave theory (U.S. Army Corps of Engineers, 1984). The term in the denominator is the wave steepness (H/L), which incorporates the wave period.

The surf similarity parameter is becoming increasingly popular in coastal engineering literature for quantifying wave effects, due to the inclusion of the (1) wave height, (2) wave period, and (3) slope of the structure or bottom, all in one dimensionless parameter. The surf similarity parameter can be used to determine whether breaking or non-breaking waves are occurring, and what type of breaking wave is expected. This dimensionless parameter also is used to determine the wave runup on a structure, which then can be used to determine the wave overtopping of a structure (U.S. Army Corps of Engineers, 1984); and for breakwater structural stability (van der Meer, 1987).

WAVE ATTENUATION

The primary purpose of a breakwater is to reduce the wave energy in its lee. The term “wave transmission” is used in reference to the wave energy that does travel past a breakwater, either by passing through and/or by overtopping the structure (U.S. Army Corps of Engineers, 1984). The wave energy that is attenuated in the lee of the breakwater is either dissipated by the structure (such as by friction, wave breaking, armor unit movement, etc.) or reflected back as reflected wave energy.

The effectiveness of a breakwater in attenuating wave energy can be measured by the amount of wave energy that is transmitted past the structure. The greater the wave transmission coefficient, the less the wave attenuation. Wave transmission is quantified by the use of the wave transmission coefficient,

[5.]

where K_t is the wave transmission coefficient, H_t is the height of the transmitted wave on the landward side of the structure, and H_i is the height of the incident wave on the seaward side of the structure (U.S. Army Corps of Engineers, 1984). Ahrens (1987) defines the wave transmission coefficient differently, using the wave height on the landward side of the structure that would occur in the absence of the structure, in place of the incident wave height on the seaward side of the structure, so that

[6.],

where H_c is the wave height measured at the same location as H_t, but without the breakwater present.

For submerged breakwaters and artificial reefs, the greater the submergence, the less the wave energy will impact the structure, and the less effective the structure will be for wave attenuation. The Shore Protection Manual (U.S. Army Corps of Engineers, 1984) presents numerous graphs of empirical data from wave tank tests that can be used to determine wave transmission coefficients.

Ahrens (1987) presents an empirical formula for subaerial breakwaters, where the crest of the structure is above the still water level and the ratio of freeboard to the incident wave height is greater than one (F/H > 1.0) as follows:

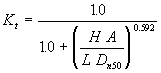[7.],

where H is the incident wave height, A is the cross sectional area of the breakwater, L is the wavelength calculated using linear wave theory for the depth = d, and D_n50 is the nominal armor unit diameter of the median size (50%) armor unit given by:

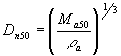[8.],

where M_a50 is the mass of the median size armor unit and r_a is the mass density of the armor material.

Ahrens (1987) presents an empirical formula for “reef breakwaters” where the ratio of the freeboard to the incident wave height is less than one (F/H < 1.0), as

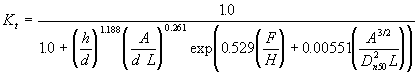[9.].

The dimensionless terms in parentheses in the denominator are the relative structure height (h/d), the ratio of the structure cross-sectional area to the product of the water depth and wavelength (A/dL), the relative freeboard (defined in Equation 3 as the ratio of the freeboard to the incident wave height, F/H which is the most influential variable according to Ahrens, 1987), and the ratio of the breakwater cross-sectional area raised to the 1.5 power divided by the product of the median armor unit diameter squared and the wavelength.

Seabrook (1997) performed extensive physical modeling tests of submerged breakwaters, using various depths of submergence, crest widths, water depths, and incident wave conditions. From that data he developed the following design equation for wave transmission at submerged rubble mound breakwaters:

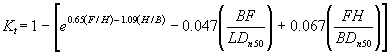[10.].

When using equations 8 and 9 the terms containing the nominal armor unit diameter, D_n50 are often found to be negligible compared to the other terms. This is especially true for Seabrook’s relationship in Equation 10, as the freeboard approaches zero as the structure crest approaches the still water level.

Wave transmission coefficients using equations 9 and 10 were calculated for the design of a submerged breakwater using Reef Ball^TM artificial reef units. The breakwater design incorporates Reef Ball units placed offshore in rows. The Reef Ball units are 1.2m high and placed in water depth of 1.4m so that the freeboard = F = -0.2m. Calculations were performed using 4, 5, and 6 rows of Reef Ball units and for various wave heights and periods. Equation 9 resulted in Ahren’s relationship predicting transmission coefficients that did not vary much with varying the number of rows of units or with varying wave conditions. The wave transmission coefficients K_t only varied from 0.64 to 0.73 which is only a wave height reduction of 36% to 27%. This predicted wave attenuation is much less that that observed due to the 3-row Reef Ball submerged breakwater in the Dominican Republic.

The results using Equation 10 are shown in Table 1 below, with Seabrook’s formula predicting wave transmission coefficients. Note that these values are more indicative of observations of the Dominican Republic Reef Ball submerged breakwater.

Table 1. Wave Transmission Coefficients from Equation 10
wave height = H (meters)	4 rows	5 rows	6 rows
0.50	0.33	0.31	0.30
0.75	0.31	0.29	0.27
1.00	0.33	0.29	0.27
1.25	0.36	0.31	0.28
1.50	0.39	0.34	0.30

Equation 10 was derived from wave tank physical model tests using rubble mound armor stone, not Reef Ball units, so that the results provide more of a design guidance and comparison than actual expected wave transmission. The values in Table 1 show that in order to reduce the wave heights by at least 70% for all of the given wave conditions, 6 rows of Reef Ball units are required. This is the recommended minimum width of the Reef Ball breakwater for wave attenuation sufficient to provide shoreline stabilization in the project area. Five rows of Reef Ball units reduce the wave heights by 66% providing slightly less effective wave attenuation and shoreline protection. Four rows reduce the wave height by 61%, which is less than that recommended for adequate shoreline stabilization.